Efficient Multi-Task and Multi-Robot Learning
Can robots learn from each other? Is sharing information between robots beneficial? Robots should be able to learn from few demonstrations of a task, and generalize to new tasks in an efficient way. They should also be able to transfer learned experiences to different robots such that the latter can achieve high performance without having to learn from scratch. We explore these questions from a theoretical point of view as well as through experiments.
Related Publications
In the robotics literature, different knowledge transfer approaches have been proposed to leverage the experience from a source task or robot—real or virtual—to accelerate the learning process on a new task or robot. A commonly made but infrequently examined assumption is that incorporating experience from a source task or robot will be beneficial. For practical applications, inappropriate knowledge transfer can result in negative transfer or unsafe behaviour. In this work, inspired by a system gap metric from robust control theory, the nu-gap, we present a data-efficient algorithm for estimating the similarity between pairs of robot systems. In a multi-source inter-robot transfer learning setup, we show that this similarity metric allows us to predict relative transfer performance and thus informatively select experiences from a source robot before knowledge transfer. We demonstrate our approach with quadrotor experiments, where we transfer an inverse dynamics model from a real or virtual source quadrotor to enhance the tracking performance of a target quadrotor on arbitrary hand-drawn trajectories. We show that selecting experiences based on the proposed similarity metric effectively facilitates the learning of the target quadrotor, improving performance by 62\% compared to a poorly selected experience.
@INPROCEEDINGS{sorocky-icra20,
author = {Michael J. Sorocky and Siqi Zhou and Angela P. Schoellig},
title = {Experience Selection Using Dynamics Similarity for Efficient Multi-Source Transfer Learning Between Robots},
booktitle = {{Proc. of the IEEE International Conference on Robotics and Automation (ICRA)}},
year = {2020},
pages = {2739--2745},
urllink = {https://ieeexplore.ieee.org/document/9196744},
urlvideo = {https://youtu.be/8m3mOkljujM},
abstract = {In the robotics literature, different knowledge transfer approaches have been proposed to leverage the experience from a source task or robot—real or virtual—to accelerate the learning process on a new task or robot. A commonly made but infrequently examined assumption is that incorporating experience from a source task or robot will be beneficial. For practical applications, inappropriate knowledge transfer can result in negative transfer or unsafe behaviour. In this work, inspired by a system gap metric from robust control theory, the nu-gap, we present a data-efficient algorithm for estimating the similarity between pairs of robot systems. In a multi-source inter-robot transfer learning setup, we show that this similarity metric allows us to predict relative transfer performance and thus informatively select experiences from a source robot before knowledge transfer. We demonstrate our approach with quadrotor experiments, where we transfer an inverse dynamics model from a real or virtual source quadrotor to enhance the tracking performance of a target quadrotor on arbitrary hand-drawn trajectories. We show that selecting experiences based on the proposed similarity metric effectively facilitates the learning of the target quadrotor, improving performance by 62\% compared to a poorly selected experience.},
} Data-efficient multi-robot, multi-task transfer learning for trajectory trackingK. Pereida, M. K. Helwa, and A. P. SchoelligAbstract and Poster, in Proc. of the Resilient Robot Teams Workshop at the IEEE International Conference on Robotics and Automation (ICRA), 2019.
![]()
![]()
![]()
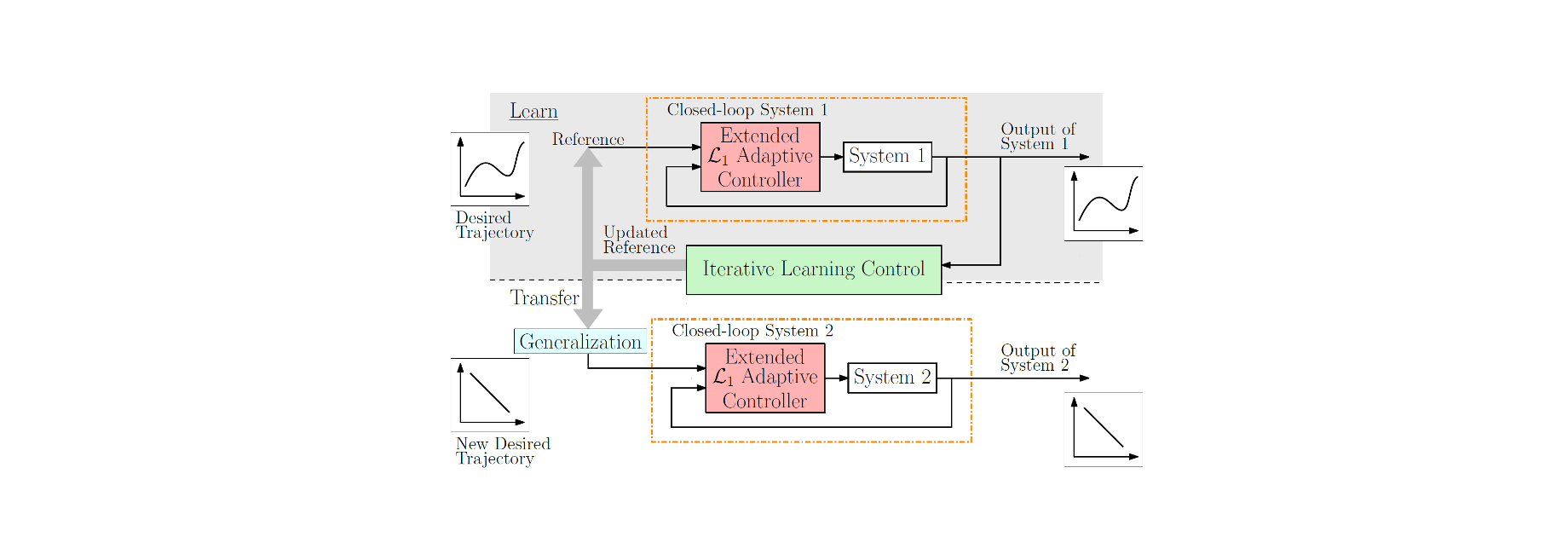
Learning can significantly improve the performance of robots in uncertain and changing environments; however, typical learning approaches need to start a new learning process for each new task or robot as transferring knowledge is cumbersome or not possible. In this work, we introduce a multi-robot, multi-task transfer learning framework that allows a system to complete a task by learning from a few demonstrations of another task executed on a different system. We focus on the trajectory tracking problem where each trajectory represents a different task. The proposed learning control architecture has two stages: (i) \emph{multi-robot} transfer learning framework that combines $\mathcal{L}_1$ adaptive control and iterative learning control, where the key idea is that the adaptive controller forces dynamically different systems to behave as a specified reference model; and (ii) a \emph{multi-task} transfer learning framework that uses theoretical control results (e.g., the concept of vector relative degree) to learn a map from desired trajectories to the inputs that make the system track these trajectories with high accuracy. This map is used to calculate the inputs for a new, unseen trajectory. We conduct experiments on two different quadrotor platforms and six different trajectories where we show that using information from tracking a single trajectory learned by one quadrotor reduces, on average, the first-iteration tracking error on another quadrotor by 74\%.
@MISC{pereida-icra19c,
author = {Karime Pereida and Mohamed K. Helwa and Angela P. Schoellig},
title = {Data-Efficient Multi-Robot, Multi-Task Transfer Learning for Trajectory Tracking},
year = {2019},
howpublished = {Abstract and Poster, in Proc. of the Resilient Robot Teams Workshop at the IEEE International Conference on Robotics and Automation (ICRA)},
abstract = {Learning can significantly improve the performance of robots in uncertain and changing environments; however, typical learning approaches need to start a new learning process for each new task or robot as transferring knowledge is cumbersome or not possible. In this work, we introduce a multi-robot, multi-task transfer learning framework that allows a system to complete a task by learning from a few demonstrations of another task executed on a different system. We focus on the trajectory tracking problem where each trajectory represents a different task. The proposed learning control architecture has two stages: (i) \emph{multi-robot} transfer learning framework that combines $\mathcal{L}_1$ adaptive control and iterative learning control, where the key idea is that the adaptive controller forces dynamically different systems to behave as a specified reference model; and (ii) a \emph{multi-task} transfer learning framework that uses theoretical control results (e.g., the concept of vector relative degree) to learn a map from desired trajectories to the inputs that make the system track these trajectories with high accuracy. This map is used to calculate the inputs for a new, unseen trajectory. We conduct experiments on two different quadrotor platforms and six different trajectories where we show that using information from tracking a single trajectory learned by one quadrotor reduces, on average, the first-iteration tracking error on another quadrotor by 74\%.},
} ![]() Data-efficient multi-robot, multi-task transfer learning for trajectory trackingK. Pereida, M. K. Helwa, and A. P. SchoelligIEEE Robotics and Automation Letters, vol. 3, iss. 2, p. 1260–1267, 2018.
Data-efficient multi-robot, multi-task transfer learning for trajectory trackingK. Pereida, M. K. Helwa, and A. P. SchoelligIEEE Robotics and Automation Letters, vol. 3, iss. 2, p. 1260–1267, 2018.
![]()
![]()
![]()
![]()
Transfer learning has the potential to reduce the burden of data collection and to decrease the unavoidable risks of the training phase. In this paper, we introduce a multi-robot, multi-task transfer learning framework that allows a system to complete a task by learning from a few demonstrations of another task executed on another system. We focus on the trajectory tracking problem where each trajectory represents a different task, since many robotic tasks can be described as a trajectory tracking problem. The proposed, multi-robot transfer learning framework is based on a combined L1 adaptive control and iterative learning control approach. The key idea is that the adaptive controller forces dynamically different systems to behave as a specified reference model. The proposed multi-task transfer learning framework uses theoretical control results (e.g., the concept of vector relative degree) to learn a map from desired trajectories to the inputs that make the system track these trajectories with high accuracy. This map is used to calculate the inputs for a new, unseen trajectory. Experimental results using two different quadrotor platforms and six different trajectories show that, on average, the proposed framework reduces the first-iteration tracking error by 74% when information from tracking a different, single trajectory on a different quadrotor is utilized.
@article{pereida-ral18,
title = {Data-Efficient Multi-Robot, Multi-Task Transfer Learning for Trajectory Tracking},
author = {Karime Pereida and Mohamed K. Helwa and Angela P. Schoellig},
journal = {{IEEE Robotics and Automation Letters}},
year = {2018},
volume = {3},
number = {2},
doi = {10.1109/LRA.2018.2795653},
pages = {1260--1267},
urllink = {http://ieeexplore.ieee.org/abstract/document/8264705/},
abstract = {Transfer learning has the potential to reduce the burden of data collection and to decrease the unavoidable risks of the training phase. In this paper, we introduce a multi-robot, multi-task transfer learning framework that allows a system to complete a task by learning from a few demonstrations of another task executed on another system. We focus on the trajectory tracking problem where each trajectory represents a different task, since many robotic tasks can be described as a trajectory tracking problem. The proposed, multi-robot transfer learning framework is based on a combined L1 adaptive control and iterative learning control approach. The key idea is that the adaptive controller forces dynamically different systems to behave as a specified reference model. The proposed multi-task transfer learning framework uses theoretical control results (e.g., the concept of vector relative degree) to learn a map from desired trajectories to the inputs that make the system track these trajectories with high accuracy. This map is used to calculate the inputs for a new, unseen trajectory. Experimental results using two different quadrotor platforms and six different trajectories show that, on average, the proposed framework reduces the first-iteration tracking error by 74% when information from tracking a different, single trajectory on a different quadrotor is utilized.},
} ![]() Multi-robot transfer learning: a dynamical system perspectiveM. K. Helwa and A. P. Schoelligin Proc. of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2017, pp. 4702-4708.
Multi-robot transfer learning: a dynamical system perspectiveM. K. Helwa and A. P. Schoelligin Proc. of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2017, pp. 4702-4708.
![]()
![]()
![]()
![]()
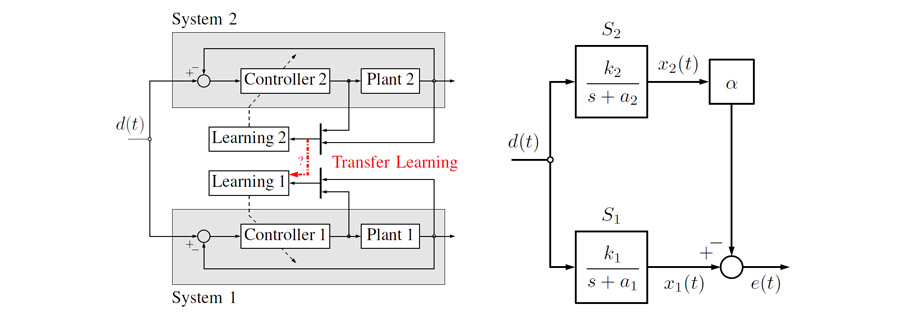
Multi-robot transfer learning allows a robot to use data generated by a second, similar robot to improve its own behavior. The potential advantages are reducing the time of training and the unavoidable risks that exist during the training phase. Transfer learning algorithms aim to find an optimal transfer map between different robots. In this paper, we investigate, through a theoretical study of single-input single-output (SISO) systems, the properties of such optimal transfer maps. We first show that the optimal transfer learning map is, in general, a dynamic system. The main contribution of the paper is to provide an algorithm for determining the properties of this optimal dynamic map including its order and regressors (i.e., the variables it depends on). The proposed algorithm does not require detailed knowledge of the robots’ dynamics, but relies on basic system properties easily obtainable through simple experimental tests. We validate the proposed algorithm experimentally through an example of transfer learning between two different quadrotor platforms. Experimental results show that an optimal dynamic map, with correct properties obtained from our proposed algorithm, achieves 60-70% reduction of transfer learning error compared to the cases when the data is directly transferred or transferred using an optimal static map.
@INPROCEEDINGS{helwa-iros17,
author={Mohamed K. Helwa and Angela P. Schoellig},
title={Multi-Robot Transfer Learning: A Dynamical System Perspective},
booktitle={{Proc. of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS)}},
year={2017},
pages={4702-4708},
doi={10.1109/IROS.2017.8206342},
urllink={https://arxiv.org/abs/1707.08689},
abstract={Multi-robot transfer learning allows a robot to use data generated by a second, similar robot to improve its own behavior. The potential advantages are reducing the time of training and the unavoidable risks that exist during the training phase. Transfer learning algorithms aim to find an optimal transfer map between different robots. In this paper, we investigate, through a theoretical study of single-input single-output (SISO) systems, the properties of such optimal transfer maps. We first show that the optimal transfer learning map is, in general, a dynamic system. The main contribution of the paper is to provide an algorithm for determining the properties of this optimal dynamic map including its order and regressors (i.e., the variables it depends on). The proposed algorithm does not require detailed knowledge of the robots’ dynamics, but relies on basic system properties easily obtainable through simple experimental tests. We validate the proposed algorithm experimentally through an example of transfer learning between two different quadrotor platforms. Experimental results show that an optimal dynamic map, with correct properties obtained from our proposed algorithm, achieves 60-70% reduction of transfer learning error compared to the cases when the data is directly transferred or transferred using an optimal static map.},
} ![]() High-precision trajectory tracking in changing environments through L1 adaptive feedback and iterative learningK. Pereida, R. R. P. R. Duivenvoorden, and A. P. Schoelligin Proc. of the IEEE International Conference on Robotics and Automation (ICRA), 2017, p. 344–350.
High-precision trajectory tracking in changing environments through L1 adaptive feedback and iterative learningK. Pereida, R. R. P. R. Duivenvoorden, and A. P. Schoelligin Proc. of the IEEE International Conference on Robotics and Automation (ICRA), 2017, p. 344–350.
![]()
![]()
![]()
![]()
![]()
As robots and other automated systems are introduced to unknown and dynamic environments, robust and adaptive control strategies are required to cope with disturbances, unmodeled dynamics and parametric uncertainties. In this paper, we propose and provide theoretical proofs of a combined L1 adaptive feedback and iterative learning control (ILC) framework to improve trajectory tracking of a system subject to unknown and changing disturbances. The L1 adaptive controller forces the system to behave in a repeatable, predefined way, even in the presence of unknown and changing disturbances; however, this does not imply that perfect trajectory tracking is achieved. ILC improves the tracking performance based on experience from previous executions. The performance of ILC is limited by the robustness and repeatability of the underlying system, which, in this approach, is handled by the L1 adaptive controller. In particular, we are able to generalize learned trajectories across different system configurations because the L1 adaptive controller handles the underlying changes in the system. We demonstrate the improved trajectory tracking performance and generalization capabilities of the combined method compared to pure ILC in experiments with a quadrotor subject to unknown, dynamic disturbances. This is the first work to show L1 adaptive control combined with ILC in experiment.
@INPROCEEDINGS{pereida-icra17,
author = {Karime Pereida and Rikky R. P. R. Duivenvoorden and Angela P. Schoellig},
title = {High-precision trajectory tracking in changing environments through {L1} adaptive feedback and iterative learning},
booktitle = {{Proc. of the IEEE International Conference on Robotics and Automation (ICRA)}},
year = {2017},
pages = {344--350},
doi = {10.1109/ICRA.2017.7989041},
urllink = {http://ieeexplore.ieee.org/abstract/document/7989044/},
urlslides = {../../wp-content/papercite-data/slides/pereida-icra17-slides.pdf},
abstract = {As robots and other automated systems are introduced to unknown and dynamic environments, robust and adaptive control strategies are required to cope with disturbances, unmodeled dynamics and parametric uncertainties. In this paper, we propose and provide theoretical proofs of a combined L1 adaptive feedback and iterative learning control (ILC) framework to improve trajectory tracking of a system subject to unknown and changing disturbances. The L1 adaptive controller forces the system to behave in a repeatable, predefined way, even in the presence of unknown and changing disturbances; however, this does not imply that perfect trajectory tracking is achieved. ILC improves the tracking performance based on experience from previous executions. The performance of ILC is limited by the robustness and repeatability of the underlying system, which, in this approach, is handled by the L1 adaptive controller. In particular, we are able to generalize learned trajectories across different system configurations because the L1 adaptive controller handles the underlying changes in the system. We demonstrate the improved trajectory tracking performance and generalization capabilities of the combined method compared to pure ILC in experiments with a quadrotor subject to unknown, dynamic disturbances. This is the first work to show L1 adaptive control combined with ILC in experiment.},
} ![]() Distributed iterative learning control for a team of quadrotorsA. Hock and A. P. Schoelligin Proc. of the IEEE Conference on Decision and Control (CDC), 2016, pp. 4640-4646.
Distributed iterative learning control for a team of quadrotorsA. Hock and A. P. Schoelligin Proc. of the IEEE Conference on Decision and Control (CDC), 2016, pp. 4640-4646.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The goal of this work is to enable a team of quadrotors to learn how to accurately track a desired trajectory while holding a given formation. We solve this problem in a distributed manner, where each vehicle has only access to the information of its neighbors. The desired trajectory is only available to one (or few) vehicles. We present a distributed iterative learning control (ILC) approach where each vehicle learns from the experience of its own and its neighbors’ previous task repetitions, and adapts its feedforward input to improve performance. Existing algorithms are extended in theory to make them more applicable to real-world experiments. In particular, we prove stability for any causal learning function with gains chosen according to a simple scalar condition. Previous proofs were restricted to a specific learning function that only depends on the tracking error derivative (D-type ILC). Our extension provides more degrees of freedom in the ILC design and, as a result, better performance can be achieved. We also show that stability is not affected by a linear dynamic coupling between neighbors. This allows us to use an additional consensus feedback controller to compensate for non-repetitive disturbances. Experiments with two quadrotors attest the effectiveness of the proposed distributed multi-agent ILC approach. This is the first work to show distributed ILC in experiment.
@INPROCEEDINGS{hock-cdc16,
author = {Andreas Hock and Angela P. Schoellig},
title = {Distributed iterative learning control for a team of quadrotors},
booktitle = {{Proc. of the IEEE Conference on Decision and Control (CDC)}},
year = {2016},
pages = {4640-4646},
doi = {10.1109/CDC.2016.7798976},
urllink = {http://arxiv.org/ads/1603.05933},
urlvideo = {https://youtu.be/Qw598DRw6-Q},
urlvideo2 = {https://youtu.be/JppRu26eZgI},
urlslides = {../../wp-content/papercite-data/slides/hock-cdc16-slides.pdf},
abstract = {The goal of this work is to enable a team of quadrotors to learn how to accurately track a desired trajectory while holding a given formation. We solve this problem in a distributed manner, where each vehicle has only access to the information of its neighbors. The desired trajectory is only available to one (or few) vehicles. We present a distributed iterative learning control (ILC) approach where each vehicle learns from the experience of its own and its neighbors’ previous task repetitions, and adapts its feedforward input to improve performance. Existing algorithms are extended in theory to make them more applicable to real-world experiments. In particular, we prove stability for any causal learning function with gains chosen according to a simple scalar condition. Previous proofs were restricted to a specific learning function that only depends on the tracking error derivative (D-type ILC). Our extension provides more degrees of freedom in the ILC design and, as a result, better performance can be achieved. We also show that stability is not affected by a linear dynamic coupling between neighbors. This allows us to use an additional consensus feedback controller to compensate for non-repetitive disturbances. Experiments with two quadrotors attest the effectiveness of the proposed distributed multi-agent ILC approach. This is the first work to show distributed ILC in experiment.},
} ![]() An upper bound on the error of alignment-based transfer learning between two linear, time-invariant, scalar systemsK. V. Raimalwala, B. A. Francis, and A. P. Schoelligin Proc. of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2015, p. 5253–5258.
An upper bound on the error of alignment-based transfer learning between two linear, time-invariant, scalar systemsK. V. Raimalwala, B. A. Francis, and A. P. Schoelligin Proc. of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2015, p. 5253–5258.
![]()
![]()
![]()
![]()
Methods from machine learning have successfully been used to improve the performance of control systems in cases when accurate models of the system or the environment are not available. These methods require the use of data generated from physical trials. Transfer Learning (TL) allows for this data to come from a different, similar system. This paper studies a simplified TL scenario with the goal of understanding in which cases a simple, alignment-based transfer of data is possible and beneficial. Two linear, time-invariant (LTI), single-input, single-output systems are tasked to follow the same reference signal. A scalar, LTI transformation is applied to the output from a source system to align with the output from a target system. An upper bound on the 2-norm of the transformation error is derived for a large set of reference signals and is minimized with respect to the transformation scalar. Analysis shows that the minimized error bound is reduced for systems with poles that lie close to each other (that is, for systems with similar response times). This criterion is relaxed for systems with poles that have a larger negative real part (that is, for stable systems with fast response), meaning that poles can be further apart for the same minimized error bound. Additionally, numerical results show that using the reference signal as input to the transformation reduces the minimized bound further.
@INPROCEEDINGS{raimalwala-iros15,
author = {Kaizad V. Raimalwala and Bruce A. Francis and Angela P. Schoellig},
title = {An upper bound on the error of alignment-based transfer learning between two linear, time-invariant, scalar systems},
booktitle = {{Proc. of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS)}},
pages = {5253--5258},
year = {2015},
doi = {10.1109/IROS.2015.7354118},
urllink = {http://hdl.handle.net/1807/69365},
note = {},
abstract = {Methods from machine learning have successfully been used to improve the performance of control systems in cases when accurate models of the system or the environment are not available. These methods require the use of data generated from physical trials. Transfer Learning (TL) allows for this data to come from a different, similar system. This paper studies a simplified TL scenario with the goal of understanding in which cases a simple, alignment-based transfer of data is possible and beneficial. Two linear, time-invariant (LTI), single-input, single-output systems are tasked to follow the same reference signal. A scalar, LTI transformation is applied to the output from a source system to align with the output from a target system. An upper bound on the 2-norm of the transformation error is derived for a large set of reference signals and is minimized with respect to the transformation scalar. Analysis shows that the minimized error bound is reduced for systems with poles that lie close to each other (that is, for systems with similar response times). This criterion is relaxed for systems with poles that have a larger negative real part (that is, for stable systems with fast response), meaning that poles can be further apart for the same minimized error bound. Additionally, numerical results show that using the reference signal as input to the transformation reduces the minimized bound further.}
} ![]() Limited benefit of joint estimation in multi-agent iterative learningA. P. Schoellig, J. Alonso-Mora, and R. D’AndreaAsian Journal of Control, vol. 14, iss. 3, pp. 613-623, 2012.
Limited benefit of joint estimation in multi-agent iterative learningA. P. Schoellig, J. Alonso-Mora, and R. D’AndreaAsian Journal of Control, vol. 14, iss. 3, pp. 613-623, 2012.
![]()
![]()
![]()
![]()
![]()
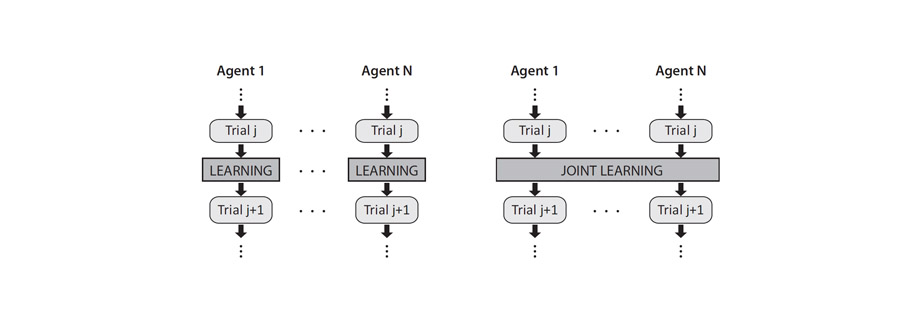
This paper studies iterative learning control (ILC) in a multi-agent framework, wherein a group of agents simultaneously and repeatedly perform the same task. Assuming similarity between the agents, we investigate whether exchanging information between the agents improves an individual’s learning performance. That is, does an individual agent benefit from the experience of the other agents? We consider the multi-agent iterative learning problem as a two-step process of: first, estimating the repetitive disturbance of each agent; and second, correcting for it. We present a comparison of an agent’s disturbance estimate in the case of (I) independent estimation, where each agent has access only to its own measurement, and (II) joint estimation, where information of all agents is globally accessible. When the agents are identical and noise comes from measurement only, joint estimation yields a noticeable improvement in performance. However, when process noise is encountered or when the agents have an individual disturbance component, the benefit of joint estimation is negligible.
@ARTICLE{schoellig-ajc12,
author = {Angela P. Schoellig and Javier Alonso-Mora and Raffaello D'Andrea},
title = {Limited benefit of joint estimation in multi-agent iterative learning},
journal = {{Asian Journal of Control}},
volume = {14},
number = {3},
pages = {613-623},
year = {2012},
doi = {10.1002/asjc.398},
urldata={../../wp-content/papercite-data/data/schoellig-ajc12-files.zip},
urlslides={../../wp-content/papercite-data/slides/schoellig-ajc12-slides.pdf},
abstract = {This paper studies iterative learning control (ILC) in a multi-agent framework, wherein a group of agents simultaneously and repeatedly perform the same task. Assuming similarity between the agents, we investigate whether exchanging information between the agents improves an individual's learning performance. That is, does an individual agent benefit from the experience of the other agents? We consider the multi-agent iterative learning problem as a two-step process of: first, estimating the repetitive disturbance of each agent; and second, correcting for it. We present a comparison of an agent's disturbance estimate in the case of (I) independent estimation, where each agent has access only to its own measurement, and (II) joint estimation, where information of all agents is globally accessible. When the agents are identical and noise comes from measurement only, joint estimation yields a noticeable improvement in performance. However, when process noise is encountered or when the agents have an individual disturbance component, the benefit of joint estimation is negligible.}
} ![]() Sensitivity of joint estimation in multi-agent iterative learning controlA. P. Schoellig and R. D’Andreain Proc. of the IFAC (International Federation of Automatic Control) World Congress, 2011, pp. 1204-1212.
Sensitivity of joint estimation in multi-agent iterative learning controlA. P. Schoellig and R. D’Andreain Proc. of the IFAC (International Federation of Automatic Control) World Congress, 2011, pp. 1204-1212.
![]()
![]()
![]()
![]()
![]()
We consider a group of agents that simultaneously learn the same task, and revisit a previously developed algorithm, where agents share their information and learn jointly. We have already shown that, as compared to an independent learning model that disregards the information of the other agents, and when assuming similarity between the agents, a joint algorithm improves the learning performance of an individual agent. We now revisit the joint learning algorithm to determine its sensitivity to the underlying assumption of similarity between agents. We note that an incorrect assumption about the agents’ degree of similarity degrades the performance of the joint learning scheme. The degradation is particularly acute if we assume that the agents are more similar than they are in reality; in this case, a joint learning scheme can result in a poorer performance than the independent learning algorithm. In the worst case (when we assume that the agents are identical, but they are, in reality, not) the joint learning does not even converge to the correct value. We conclude that, when applying the joint algorithm, it is crucial not to overestimate the similarity of the agents; otherwise, a learning scheme that is independent of the similarity assumption is preferable.
@INPROCEEDINGS{schoellig-ifac11,
author = {Angela P. Schoellig and Raffaello D'Andrea},
title = {Sensitivity of joint estimation in multi-agent iterative learning control},
booktitle = {{Proc. of the IFAC (International Federation of Automatic Control) World Congress}},
pages = {1204-1212},
year = {2011},
doi = {10.3182/20110828-6-IT-1002.03687},
urlslides = {../../wp-content/papercite-data/slides/schoellig-ifac11-slides.pdf},
urldata = {../../wp-content/papercite-data/data/schoellig-ifac11-files.zip},
abstract = {We consider a group of agents that simultaneously learn the same task, and revisit a previously developed algorithm, where agents share their information and learn jointly. We have already shown that, as compared to an independent learning model that disregards the information of the other agents, and when assuming similarity between the agents, a joint algorithm improves the learning performance of an individual agent. We now revisit the joint learning algorithm to determine its sensitivity to the underlying assumption of similarity between agents. We note that an incorrect assumption about the agents' degree of similarity degrades the performance of the joint learning scheme. The degradation is particularly acute if we assume that the agents are more similar than they are in reality; in this case, a joint learning scheme can result in a poorer performance than the independent learning algorithm. In the worst case (when we assume that the agents are identical, but they are, in reality, not) the joint learning does not even converge to the correct value. We conclude that, when applying the joint algorithm, it is crucial not to overestimate the similarity of the agents; otherwise, a learning scheme that is independent of the similarity assumption is preferable.}
}